Maurits Cornelis ESCHER

Maurits Cornelis Escher nacque a Leeuwarden (Paesi Bassi) nel 1898; era figlio di un ingegnere e fece i suoi studi al Technical College di Delft ed alla Scuola di Architettura ed Arti decorative di Haarlem. Da qui, sotto la guida del grafico portoghese Samuel Jesserun de Mesquita, sorse la sua passione per la xilografia (tecnica di incisione dei disegni su una superficie di legno duro, dalla quale si ricavano le stampe su carta). Dal 1922 al 1935 Escher visse in Italia e, nell'estate del 1923 a Ravello, conobbe Jetta Umiker, figlia di un industriale svizzero. Nel 1936 Escher sposo' Jetta e, in sua compagnia, visito' la moschea di Cordoba e l'Alhambra, fortezza araba di Granada, della quale rimase fortemente colpito soprattutto per gli ornamenti moreschi del palazzo. Nel 1935 fu costretto dal fascismo a scappare in Svizzera, dove inizio' i suoi studi sulla prospettiva e sulle illusioni ottiche. Da allora si dedico' ai disegni astratti e smise di produrre opere paesaggistiche, nelle quali apparivano i tipici paesaggi dell'Italia meridionale e delle zone costiere del Mediterraneo. Nel 1937 si trasferi' a Bruxelles e, dopo l'invasione tedesca, si stabili' definitivamente in Olanda. Il 1937 fu un anno indicativo per la produzione dei suoi lavori; infatti, da quel momento in poi, fu conquistato da simmetrie, strutture matematiche, continuita', infinito e dal problema, sempre presente in ogni suo quadro, riguardante la riproduzione delle tre dimensioni su di una superficie bidimensionale.

Le opere di Escher possono essere suddivise in quattro periodi:


Periodo dei paesaggi o periodo italiano: Compenetrazione di mondi

Vedere mondi diversi nello stesso identico luogo e nello stesso tempo.

A partire dal 1934 Escher inizio' a progettare composizioni artistiche con le quali si potesse giungere a rappresentare una “simultaneita' di presenze”. A tal proposito, un aiuto significativo gli fu dato dai riflessi di specchi convessi. In essi l'occhio, per mezzo di una semplice costruzione derivata dalla geometria ottica, vede l'immagine riflessa dell'intero Universo; cio' che resta celato e' soltanto quello che viene a trovarsi sul retro dello specchio. In sostanza, secondo la teoria dell'artista, uno specchio e' capace di estendere il raggio d'azione dell'occhio, evidenziando piu' angolature da cui e' possibile guardare e conoscere il mondo. Lo specchio e' dunque un elemento di connessione che, con un gioco di riflessi, puo' far convivere due o piu' mondi nello stesso luogo e nello stesso tempo. Mediante l'utilizzo di superfici riflettenti, piane e convesse, naturali ed artificiali, l'artista voleva raggiungere il suo obiettivo, ossia quello di coinvolgere, nella trasposizione della realta' su di un foglio, il contrasto esistente tra tridimensionalita' e bidimensionalita'. Escher sosteneva che uno specchio, in particolare quello piano, riproducendo una realta' tridimensionale su di una superficie a due dimensioni, creasse la suggestione della spazialita'. Percio', anche il disegno doveva dare l'illusione di vedere spazi e volumi, proprio come accade in uno specchio.

Mano con sfera riflettente (1935, Escher in Het Paleis, L'Aia, Paesi Bassi) - la litografia rappresenta cio' che l'artista percepisce direttamente, vale a dire la propria mano e quello che, senza l'ausilio della sfera, la sua vista non potrebbe raggiungere, cioe' se stesso nella stanza ampliata e deformata dalla sfera riflettente. In questo lavoro appaiono due mondi contemporaneamente. La superficie sferica viene a coincidere con l'ambiente circostante, innescando, all'interno della litografia, una dialettica tra cio' che sembra reale e cio' che invece non lo e', poiche' e' un riflesso. La descrizione in terza persona che Escher fornisce del suo autoritratto e' significativa: "Sulla mano del disegnatore c'è una sfera riflettente. In questo specchio egli vede un'immagine molto più completa dell'ambiente circostante, di quella che avrebbe attraverso una visione diretta. Lo spazio totale che lo circonda - le quattro pareti, il pavimento e il soffitto della sua camera - viene infatti rappresentato, anche se distorto e compresso, in questo piccolo disco. La sua testa, o più precisamente, il punto fra i suoi occhi, si trova nel centro. In qualsiasi direzione si giri, egli rimane il punto centrale. L'ego è invariabilmente il centro del suo mondo" (M.C.Escher, Grafica e disegni, cit., p. 13).

Una curiosita':

Osservando attentamente la litografia sembra che sia la mano sinistra di Escher a reggere la sfera; invece il grafico fa capire che cio' che in realta' si sta guardando e' la mano destra dell'artista, perche' una stampa e' speculare al disegno originale. Da questo si capisce che Escher e' mancino e quindi per disegnare egli usa la sua mano sinistra.


Periodo delle metamorfosi: Cicli


Nel volume “Grafica e disegni”, Escher racconta cosa ha stimolato la sua seconda produzione al confine tra Arte e Scienza: “Le idee che stanno alla loro base derivano dalla mia ammirazione e dal mio stupore nei confronti delle leggi che regolano il mondo in cui viviamo. Chi si meraviglia di qualcosa si rende consapevole di tale meraviglia. Nel momento in cui sono aperto e sensibile nei confronti degli enigmi che ci circondano, considerando e analizzando le mie osservazioni, entro in contatto con la matematica. Anche se non ho avuto un'istruzione o conoscenze in scienze esatte mi sento spesso più vicino ai matematici che ai miei colleghi artisti” (M.C.Escher, Grafica e disegni, Taschen Köln 1992, p.6).

Ciclo (1938, Escher in Het Paleis, L'Aia, Paesi Bassi) - in questa litografia, appartenente al periodo artistico denominato “periodo delle metamorfosi”, si puo' notare come i temi “metamorfosi e cicli” appaiano strettamente connessi. Per comprenderlo bisogna osservare attentamente l'opera; in essa si nota un omino allegro comparire da un androne di una casa; egli corre giu' dalle scale e, man mano che scende, si trasforma in una bizzarra forma geometrica. Questa metamorfosi da figura umana a figura geometrica non e' il punto terminale della composizione; difatti, guardando in alto a sinistra, la figura pian piano si trasforma in forme sempre piu' semplici, fino a raggiungere forme romboidali. Successivamente, tre rombi assumono la forma di cubi che si riducono in un unico blocco dello stesso motivo del pavimento piastrellato del piccolo cortile. Continuando ad osservare la litografia nel retro della stanzetta della casa, sembra che queste forme senza vita diventino nuovamente degli omini; infatti, l'allegro pupazzo di prima sbuca fuori ancora una volta, saltellando. In definitiva, nella litografia, esseri viventi mutano in figure geometriche inanimate trasformandosi nei mattoni che costruiscono la casa da cui lo stesso omino si affaccia. La vita si risolve cosi' in un ciclo infinito di continua perdita e riacquisto di corpo e volume.

Questa litografia sintetizza la concezione che Echer aveva del passaggio dalla superficie allo spazio e viceversa, sfruttando la possibilita' della raffigurazione. A questo proposito l'artista si esprime cosi': “il panorama della parte superiore del disegno rappresenta il massimo della naturalezza tridimensionale, mentre il motivo ricorrente della parte inferiore rappresenta la restrizione bidimensionale per eccellenza” (M.C.Escher, Grafica e disegni, cit.,p.11).

La tecnica utilizzata in questa litografia e' quella della “tassellazione o divisione regolare del piano”, che rappresenta lo strumento usato dall'artista nei suoi capolavori. Escher a questo proposito scrive: “Essa è la più ricca fonte di ispirazione da cui io abbia mai derivato le mie idee ed essa non è in nessun modo inaridita”.

Nelle sue opere, accanto alla tecnica della tassellazione del piano, Escher affianca la traslazione, la rotazione e la simmetria di un qualsiasi motivo ornamentale; percio', gli elementi che inizialmente funzionano da figure diventano ciclicamente sfondo e viceversa, senza fine. In questo modo si crea un equilibrio dinamico nel quale vi e' sempre un rapporto tra figura e sfondo.


Periodo dei quadri di prospettiva: Prospettiva


Su e Giù (1947, Escher in Het Paleis, L'Aia, Paesi Bassi) - la caratteristica della litografia e' la presenza di un unico punto di fuga, che viene utilizzato sia come Zenit che come Nadir:

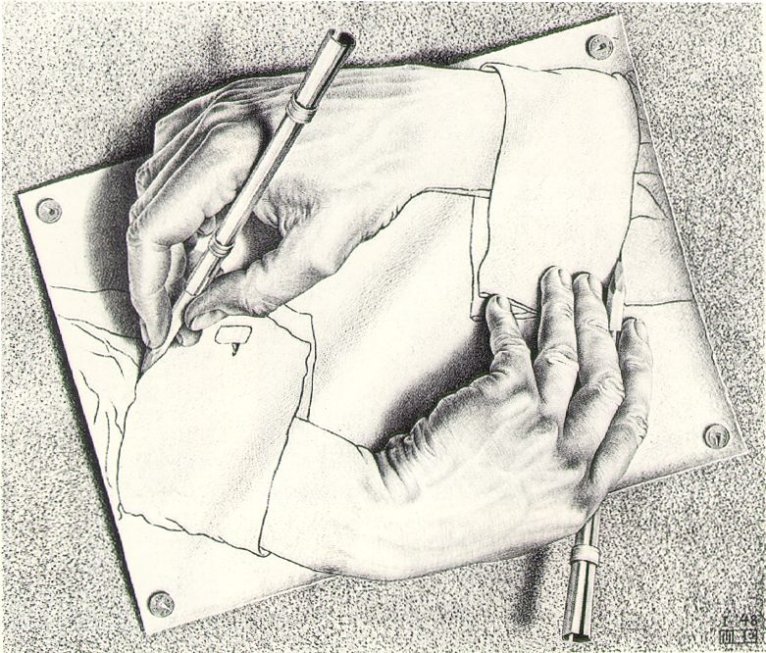Mani che disegnano (1948, Escher in Het Paleis, L'Aia, Paesi Bassi) - questa litografia raffigura due mani, ognuna impegnata a disegnare l'altra, entrambe rappresentate su un foglio di carta fissato su una tavola da disegno con delle puntine. Quest'opera e' caratterizzata da diversi elementi paradossali; il paradosso principale e' rappresentato dal circolo vizioso dell'autoreferenza, dovuto al fatto che ognuna delle mani sta disegnando l'altra. L'altro elemento contraddittorio e' il contrasto tra la tridimensionalita' delle mani e la bidimensionalita' dei polsini delle camicie. In questa litografia, come in molte altre opere, l'intento di Escher e' quello di far notare a chi osserva che ogni disegno e' una forma di illusione. Infatti, vengono suggerite le tre dimensioni sebbene sulla carta ce ne siano solo due.

Relatività (1953, Escher in Het Paleis, L'Aia, Paesi Bassi) - questa litografia ha un profondo significato e cioe': esistono piu' piani della realta', nessuno di noi se ne accorge, ma bisogna accettarne serenamente l'esistenza. In pratica, la litografia e' il risultato dell'intersezione di tre mondi completamente diversi tra loro. Infatti, le sedici figurine che entrano in scena si possono suddividere in tre gruppi, ciascuno dei quali abita un proprio mondo, vede gli oggetti in modo diverso ed ha un concetto diverso di cio' che e' orizzontale o verticale. Tuttavia, la diversita' dei tre mondi non impedisce alle figurine di usare le stesse scale e di compiere lo stesso percorso. L'intersezione di mondi diversi determina pero' l'impossibilita' della convivenza tra gli uomini che giacciono sulle diverse superfici. Essi non potranno mai uscire dal loro mondo per incontrarsi. Con quest'opera sembra che Escher voglia sottolineare come il concetto che si ha di cio' che e' reale sia relativo e sia creazione di ciascun individuo. Secondo l'artista la realta', in quanto tale, non dovrebbe avere alcun limite ed una maggiore apertura mentale consentirebbe di scoprire mondi finora inesplorati. Questo punto di vista e' molto vicino alla concezione di “surrealta'” che avevano i surrealisti. Escher induce a riflettere su come la vita non sia fatta di una cosa sola, ma sia una strana alchimia di contenuti e forme, arte e scienza, verita' e finzione, realta' e sogno, nella quale si puo' seguire una di queste cose e perdere l'altra. Cosi' come accade nelle divisioni dei piani realizzate dall'artista, dove inseguire il nero significa perdere il bianco; tuttavia e' possibile godere di una visione sintetica d'insieme che va oltre la somma delle parti.


Periodo delle approssimazioni all'infinito: Figure impossibili


Belvedere (1958, Escher in Het Paleis, L'Aia, Paesi Bassi) - in questa litografia sono evidenti i richiami all'Architettura Rinascimentale italiana, ma sono anche presenti elementi “fuori dal normale”. Uno di questi e' la posizione dei due individui che guardano dalle balconate. Infatti, la dama posizionata al piano di sopra, attraverso la facciata principale, osserva in una particolare direzione; invece l'uomo che si trova al piano di sotto, attraverso la medesima facciata, sembra osservare in tutt'altra direzione. Un altro elemento impossibile e' la scala a pioli; questa scala, al piano inferiore, parte dall'interno dell'edificio e si appoggia all'esterno del piano superiore. Per convincersi dell'impossibilita' di costruire tale edificio e' sufficiente osservare le colonne del piano inferiore, queste sembrano incrociarsi e compiere delle pericolose pieghe. Nalla litografia e' indicato chiaramente da Escher il modello matematico da lui adottato, che e' tenuto in mano dall'uomo seduto in basso sulla panca; si tratta del cubo di Necker:

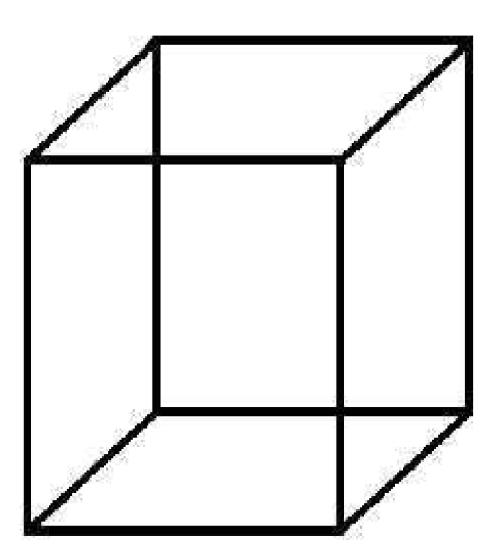
Il cubo di Necker e' una rappresentazione bidimensionale ambigua; la sua struttura a linee corrisponde ad una proiezione isometrica di un cubo. Gli incroci tra due linee non evidenziano quale linea si trovi sopra l'altra e quale sia al di sotto. In pratica, non e' possibile indicare quale faccia sia rivolta verso l'osservatore e quale sia dietro al cubo; questo permette di passare facilmente da una interpretazione all'altra fornendo ambiguita' alla rappresentazione.

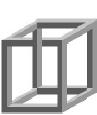cubo impossibile.

Il vero desiderio di Escher era quello di rappresentare l'infinito attraverso le tassellazioni. Uno dei suoi disegni preparatori riguardante questo aspetto, intitolato “Studio di divisione regolare del piano con rettili”, e' stato commentato dall'artista nel seguente modo: “Che cosa è stato realizzato con l’ordinata suddivisione della superficie (…)? Non ancora il vero infinito, ma comunque un frammento di esso, un pezzo dell’universo dei rettili. Se la superficie in cui essi si inseriscono fosse infinitamente grande, un numero infinito di essi potrebbe esservi rappresentato”.

L'esigenza di raggiungere la rappresentazione dell'infinito condusse Escher a produrre opere che contenevano figure ottenute mediante il rimpicciolimento progressivo. La sua insoddisfazione per i diversi tentativi di rappresentare l'infinito trovo' una risposta solo quando Escher incontro' il matematico Harold Scott Macdonald Coxeter; egli fece conoscere all'artista il cosiddetto “modello di Poincarè del piano iperbolico”, basato sulla negazione del V postulato di Euclide. In questo modello l'artista trovo' lo strumento per realizzare cio' che da tempo desiderava. Furono molti i tentativi fatti da Escher in questo senso; il primo tentativo fu l'opera dal titolo “Limite del cerchio I”, ad essa seguirono, con migliori risultati, le xilografie intitolate: “Limite del cerchio II, III e Limite del cerchio IV”. In queste ultime composizioni l'artista vide finalmente realizzata la rappresentazione dell'infinito; egli commento' cosi' il suo traguardo: “(…) il limite dell’infinitamente numeroso e dell’infinitamente piccolo viene raggiunto sul bordo circolare”. L'opera migliore in tal senso resta comunque quella dal titolo:

Limite del cerchio III (1959, Escher in Het Paleis, L'Aia, Paesi Bassi) - in questa xilografia, per avere l'idea dello spazio che Escher voleva rappresentare, bisogna porsi al centro del disegno e supporre di camminare fino al bordo. Man mano che si cammina ci si restringe sempre di piu', proprio come accade ai pesci della figura. Dunque, per raggiungere il bordo bisognerebbe percorrere una distanza che sembra proprio infinita. Questa rappresentazione dell'infinito anticipa di qualche decennio la formulazione matematica del concetto di “frattale” per opera di Benoît Mandelbrot.

Tra le piu' note e famose figure impossibili, ossia disegni che rappresentano qualcosa che non esiste nel mondo reale, utilizzate da Escher nei suoi lavori grafici del periodo delle approssimazioni all'infinito, vi e' il “triangolo impossibile di Penrose”. Questa figura fu disegnata nel 1958 da Lionel Sharples Penrose, psichiatra e genetista britannico, e da suo figlio Roger, matematico e fisico.

A prima vista il triangolo impossibile appare simile ad un triangolo equilatero ma, da un esame piu' attento, ci si rende conto che ogni angolo e' retto e che i tre angoli sono stati posti in relazione reciproca per mezzo di una disposizione spaziale impossibile nel mondo reale. Quando Escher conobbe la figura impossibile di Penrose le diede ampio risalto nella litografia dal titolo:

Cascata (1961, Escher in Het Paleis, L'Aia, Paesi Bassi) - in questa litografia Escher sfrutta la figura impossibile di Penrose per realizzare il paradossale effetto dell'acqua che “risale” nel canale. In pratica, se si osserva attentamente la litografia si nota come l'acqua che esce dal mulino “magicamente” torna in alto. Seguendo il percorso dell'acqua ci si ritrova inaspettatamente nella parte alta della torretta anteriore, la stessa da cui cade l'acqua verso il basso. L'effetto e' di sorpresa perche' non si e' avuta la percezione di compiere un percorso in salita, tanto meno di essere passati dalla zona posteriore a quella anteriore dell'edificio. La struttura essenziale della litografia presenta tre triangoli impossibili collegati tra loro; non vi sono angoli tridimensionali nel disegno, come non ve ne sono nel triangolo impossibile. In pratica, Escher distrae l'osservatore con l'abile uso della prospettiva associata alla struttura dell'edificio ed a quella del paesaggio.


L'ultima opera della vita dell'artista e' la xilografia intitolata:

Serpenti (1969, Escher in Het Paleis, L'Aia, Paesi Bassi) - in questa xilografia viene riproposto il tema della rappresentazione dell'infinito, gia' affrontato in precedenza. In questo caso pero' lo spazio si scontra con l'infinito sia nella direzione del bordo che verso il centro del cerchio, producendo un restringimento in entrambi i sensi.


Escher e' stato un artista capace di combinare meravigliosamente Arte e Scienza. I temi da lui affrontati per la realizzazione delle sue opere presentano, come denominatore comune, tre grandi scoperte scientifiche del 1900:

Images source: https://www.settemuse.it/pittori_scultori_europei/m_c_escher.htm

Per conoscere altre opere di Escher clicca sul nome dell'artista.

Per saperne di piu': Escher IN HET PALEIS


CORRENTI ARTISTICHE

FISICA E PITTURA