ENTROPIA, PROBABILITA', INFORMAZIONE


TEORIA DELL'INFORMAZIONE
« L'informazione e' la risoluzione dell'incertezza »
Claude Shannon

L'incertezza attesa, cioe' il contenuto informativo medio nel sapere che dal lancio di una moneta sia uscito testa o croce e' dato dalla formula di Shannon:
H (lancio di una moneta)=[-p(x1)log2(p(x1))]+[-p(x2)log2(p(x2))]
dove: p(x1)=p(x2)=½ (probabilita' che nel lancio della moneta esca testa o croce; si tratta di eventi equiprobabili).
H (lancio di una moneta)=-½log2½ + [-½log2½] = ½ + ½ = 1 bit (numero minimo di bit necessari per la codifica dell'evento).
Nella teoria dell'informazione l'entropia misura il grado di incertezza medio dei messaggi emessi da una sorgente. Essa rappresenta una stima del numero medio di bit necessari a codificare un messaggio proveniente da quella sorgente.
Formula di Shannon per l'entropia
L'entropia e' la sommatoria di tutti i possibili messaggi che possono essere emessi da una sorgente, calcolati ciascuno con la propria probabilita':
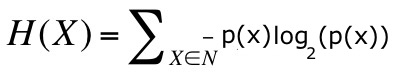
H(X): Entropia della variabile X su un insieme discreto di messaggi non equiprobabili.
p(x): probabilita' del messaggio X; 0<p(x)<1.
p(x)=0 rappresenta l'impossibilita' teorica per quell'evento di verificarsi, ossia per quel messaggio di essere emesso.
p(x)=1 rappresenta la certezza teorica.
Nella teoria dell'informazione si associa ad un basso valore di entropia una bassa quantita' di informazione, perche' quel determinato evento e' facilmente prevedibile, cioe' avra' un'alta probabilita' di manifestarsi . Invece ad un alto valore di entropia si associa una grande quantita' di informazione, perche' quel determinato evento e' imprevedibile, cioe' avra' una bassa probabilita' di manifestarsi.
In definitiva:
gli eventi certi (basso livello di entropia), non danno informazione;
gli eventi poco probabili (alto livello di entropia) danno molta informazione.
TEORIA DELL'ENTROPIA


La fusione del ghiaccio avviene con aumento di entropia: l'aria dell'ambiente circostante ed anche l'acqua, in forma liquida, trasferisce progressivamente energia termica al ghiaccio, quindi l'energia del sistema viene maggiormente dispersa ed alla fine si ha un sistema liquido completamente omogeneo. Percio', lo stato finale verso cui evolve spontaneamente il sistema eterogeneo di acqua e ghiaccio, lasciato a temperatura ambiente, e' lo stato per il quale la dispersione di energia e' elevata; tale stato e' quello con maggiore probabilita' di vericarsi spontaneamente. Ecco perche' il sistema tende spontaneamente alla massima entropia, intesa come misura del grado di dispersione e diffusione dell'energia ad una certa temperatura.
Nella teoria dell'entropia un basso livello di entropia, ossia elevato squilibrio energetico ed elevata attitudine a trasformare energia in lavoro, comporta anche minore probabilita' di un sistema di esistere con una certa energia in un particolare “macrostato”. Invece, un elevato livello di entropia indica uno stato ad alta probabilita', per il quale la dispersione di energia e' elevata.
Apparente contraddizione
Il teorico dell'informazione investiga la “probabilita' del verificarsi di una sequenza di elementi”. Per esempio, dopo che egli ha visto cento cigni bianchi considera probabile ed al tempo stesso povera d'informazione la vista di un altro cigno bianco, mentre riterrebbe improbabile e ricca d'informazione la scoperta di un cigno nero.
Il teorico dell'entropia invece non si occupa della probabilita' di successione in una serie di elementi, bensi' della “distribuzione generale dei tipi di elementi in una data distribuzione”. Il teorico dell'entropia quindi considera l'evento del vedere cento cigni bianchi dal punto di vista della sua struttura o conformazione generale, ovvero ritiene che, potendosi incontrare cigni di molti colori, il vederne cento tutti bianchi sia altamente improbabile e quindi e' portato a considerarlo come un evento ricco d'informazione.
In definitiva:
sia nella Termodinamica, sia nella Teoria dell'Informazione l'entropia e' una misura di quanto si sia degradato il contenuto utilizzabile di un sistema, un contenuto energetico nel caso termodinamico, un contenuto di informazione nel caso di un messaggio. L'informazione gioca il ruolo dell'energia disponibile.